Some Solutions to High dimensional probability (Vershynin)
I give you no guarantees on the correctness of these solutions.
1. 5.4.5
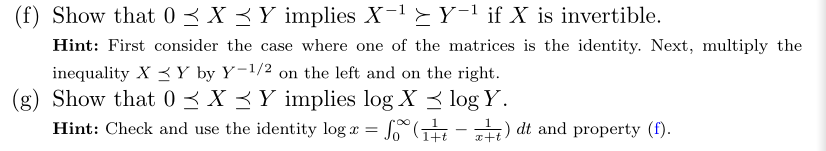
1.1. F
If \(Y = I\), then
\begin{align*} 0 &\preceq X \preceq I \\ \iff 0 &\preceq I \preceq X ^{-\frac{1 }{2 }} X ^{- \frac{1}{2}} \\ \iff 0 &\preceq I \preceq X ^{-1} \end{align*}\(X ^{-\frac{1}{2}}\) exist since \(X \succeq 0\) is positive semi-definite. Then
\begin{align*} 0 &\preceq X \preceq Y \\ \iff 0 &\preceq Y ^{-\frac{1 }{2 }} X Y ^{- \frac{1}{2}} \preceq I \\ \end{align*}Suppose \(X = Y ^{-\frac{1 }{2 }} X Y ^{- \frac{1}{2}} \)
\begin{align*} &0 \preceq I \preceq X ^{-1} \\ &0 \preceq I \preceq \left( Y ^{-\frac{1 }{2 }} X Y ^{- \frac{1}{2}} \right) ^{-1} \\ &0 \preceq I \preceq Y ^{\frac{1 }{2 }} X ^{-1} Y ^{\frac{1}{2}} \\ &0 \preceq Y ^{-\frac{1}{2}} Y ^{-\frac{1}{2}} \preceq X ^{-1}\\ &\iff Y ^{-1} \preceq X ^{-1} \end{align*}1.2. G
\begin{align*} \log \left( X \right) &= \int _{0} ^{\infty} \left( \frac{1}{1 + t } - \frac{1}{X + t} \right) dt \\ \log \left( X \right) - \log \left( Y \right) &= \int _{0} ^{\infty} \left( \frac{1}{Y + t } - \frac{1}{X + t} \right) dt \\ \log \left( X \right) - \log \left( Y \right) &= \int _{0} ^{\infty} \left( \left( Y + t \right) ^{-1} - \left( X + t \right) ^{-1} \right) dt \end{align*}
We have
\begin{align*} 0 \preceq & X \preceq Y \\ \iff t \preceq X + t &\preceq Y + t \\ \iff \left( X + t \right) ^{-1} &\succeq \left( Y + t \right) ^{-1} \\ \iff \left( Y + t \right) ^{-1} &- \left( X + t \right) ^{-1} \preceq 0 \end{align*}Hence
\begin{align*} \log \left( X \right) - \log \left( Y \right) &= \int _{0} ^{\infty} \left( \left( Y + t \right) ^{-1} - \left( X + t \right) ^{-1} \right) dt \\ \log \left( X \right) - \log \left( Y \right) &\preceq 0 \\ \log \left( X \right) &\preceq \log \left( Y \right) \end{align*}2. 5.4.11

Given the Matrix Bernstein's Inequality, where \(X_1 , \dots, X_N\) are independent, mean zero, \(n\times n\) symmetric random matrices for \(t \geq 0\). We assert that
\begin{align*} \mathbb{P} \left\{ \left\| X \right\| \geq t \right\} \leq 2 n \exp \left\{ \frac{- t^2/2}{σ^2 + K \left( \frac{t}{3} \right)} \right\} &\leq 2 e ^{-u} \\ \iff \log \left( 2 \right) + \log \left( n \right) - \frac{t^2/2}{σ^2 + K \left( \frac{t}{3} \right)} &\leq \log \left( 2 \right) - u \end{align*}Set \(t = \sqrt{2} \left[ \sqrt{ σ^2 \left( \log \left( n \right) + u \right)} + K \left( u + \log \left( n \right) \right) \right]\), then
\begin{align*} \frac{-t^2}{2} &= - \left( σ^2 \left( \log \left( n \right) + u \right) + 2K \left( \log \left( n \right) + u \right) \sqrt{ σ^2 \left( \log \left( n \right) + u \right)} + K^2 \left( \log \left( n \right) + u \right)^2 \right)\\ σ^2 + K \left( \frac{t}{3} \right) &= σ^2 + \frac{2K}{3} \left( \sqrt{\sigma ^2 \left( \log \left( n \right) + u \right) } + K \left( \log \left( n \right) + u \right) \right) \end{align*} \begin{align*} - \frac{t^2/2}{σ^2 + K \left( \frac{t}{3} \right)} &= \frac{-\left( σ^2 \left( \log \left( n \right) + u \right) + 2K σ \left( \log \left( n \right) + u \right) \sqrt{ \left( \log \left( n \right) + u \right)} + K^2 \left( \log \left( n \right) + u \right)^2 \right)} {σ^2 + \frac{2Kσ}{3} \sqrt{ \sigma ^2 \left( \log \left( n \right) + u \right) } + \frac{2K^2}{3} \left( \log \left( n \right) + u \right) } \\ &\approx -\left( \log \left( n \right) + u \right) \left( \frac{σ^2 + 2K σ \sqrt{ \log \left( n \right) + u } + K^2 \left( \log \left( n \right) + u \right) } {σ^2 + \frac{2Kσ}{3} \sqrt{\log \left( n \right) + u } + \frac{2K^2}{3} \left( \log \left( n \right) + u \right) } \right) \\ & \lesssim - \left( \log \left( n \right) + u \right) \end{align*}We can verify whether our previous assertion by
\begin{align*} \log \left( n \right) - \frac{t^2/2}{σ^2 + K \left( \frac{t}{3} \right)} &\leq -u \\ \log \left( n \right) - \left( \log \left( n \right) + u \right) &\leq - u \\ -u &\leq -u \end{align*}Since
\begin{align*} \mathbb{P} \left\{ \left\| \sum _{i=1} ^{N} X_i \right\| \geq \sqrt{2} \left( σ \sqrt{ \log \left( n \right) + u } + K \left( u + \log \left( n \right) \right) \right) \right\} &\leq \mathbb{P} \left\{ \left\| \sum _{i=1} ^{N} X_i \right\| \geq σ \sqrt{ \log \left( n \right) + u } + K \left( u + \log \left( n \right) \right) \right\} \end{align*}Then
\begin{align*} \left\| \sum _{i=1} ^{N} X_i \right\| &\leq t \\ &\leq σ \sqrt{ \log \left( n \right) + u } + K \left( u + \log \left( n \right) \right) \\ &\leq \left( \left\| \sum _{i=1} ^{N} \mathbb{E} X_i^2 \right\| \right) ^{\frac{1}{2}} \sqrt{u + \log \left( n \right)} + K \left( u + \log \left( n \right) \right) \end{align*}with probability at least \(1 - 2 e ^{-u}\). We can calculate the expectation directly by
\begin{align*} \mathbb{E} X &= \int _{0} ^{∞} \mathbb{P} \left\{ X > t \right\} dt \\ \mathbb{E} \left\| \sum _{i=1} ^{N} X_i \right\| &= \int _{0} ^{∞} \mathbb{P} \left\{ \left\| \sum _{i=1} ^{N} X_i \right\| > t \right\} dt \\ %% &= \int _{0} ^{t_0} \mathbb{P} \left\{ \left\| \sum _{i=1} ^{N} X_i \right\| \geq t \right\} dt + \int _{t_0} ^{∞} \mathbb{P} \left\{ \left\| \sum _{i=1} ^{N} X_i \right\| \geq t \right\} dt \\ &\leq \int _{0} ^{∞} 2 e ^{-u} dt \\ \text{Differentiating } u &\Longrightarrow t = σ \sqrt{ \log \left( n \right) + u } + K \left( u + \log \left( n \right) \right) \\ &\Longrightarrow \frac{dt}{du} = \frac{σ}{2} \left( \log \left( n \right) + u \right) ^{-\frac{1}{2}} + K \\ &\leq \int _{0} ^{∞} 2 e ^{-u} \left( \frac{σ}{2 \sqrt{ \log \left( n \right) + u }} +K \right) du \\ &\leq \int _{0} ^{∞} \left( \frac{ σ e ^{-u}}{ \sqrt{ u }} + 2K e ^{-u} \right) du \\ &= σ\sqrt{\pi} + 2K \\ &\lesssim σ \sqrt{ \log \left( n \right) + u } + K \left( \log \left( n \right) + u \right) \end{align*}To conclude
\begin{align*} \mathbb{E} \left\| \sum _{i=1} ^{N} X_i \right\| \lesssim \left( \left\| \sum _{i=1} ^{N} \mathbb{E} X_i^2 \right\| \right) ^{\frac{1}{2}} \sqrt{u + \log \left( n \right)} + K \left( u + \log \left( n \right) \right) \end{align*}Let \(u = 1\), then
\begin{align*} \mathbb{E} \left\| \sum _{i=1} ^{N} X_i \right\| ≲ \left\| \sum _{i=1} ^{N} \mathbb{E} X_i^2 \right\| ^{\frac{1}{2}} \sqrt{ 1 + \log \left( n \right)} + K \left( 1 + \log \left( n \right) \right) \end{align*}3. 5.4.13

3.1. A
We know that
\begin{align*} σ^2 &= \left\| \mathbb{E} \left(\sum _{i=1} ^{N} ϵ_i A_i \right)^2 \right\| \\ &= \left\| \sum _{i=1} ^{N} \sum _{j=1} ^{N} \mathbb{E} \left[ ϵ_i ϵ_j \right] A_i A_j \right\| \\ &= \left\| \sum _{i=1} ^{N} A_i ^2 \right\| \end{align*}We can approximate for the expectation directly
\begin{align*} \mathbb{E} \left\| \sum _{i=1} ^{N} ϵ_i A_i \right\| &\approx \mathbb{E} \left\| \sum _{i=1} ^{n} a_i A_i \right\| & \text{Central limit Theorem} \\ &= \mathbb{E} \left[ \max _{i=1, \dots, d} \left| a_i \right|^2 \right]\\ &\approx 2 σ^2 \log \left( n \right) \end{align*}where \(a_i\) are independent standard normal variables. Therefore
\begin{align*} \left( \mathbb{E} \left\| \sum _{i=1} ^{N} ϵ_i A_i \right\|^2 \right) ^{\frac{1}{2}} \approx \sqrt{2 σ^2 \log (n)} \end{align*}
The last approximation we can be proven as follows:
Let \(X_1 , \dots , X_n\) be a sequence of zero mean sub-Gaussian random variables with parameter \(σ\)
Since \(1 + \log \left( n \right) \geq 2 \log \left( n \right)\) for \(n \geq 1\), we can conclude the proof
\begin{align*} \mathbb{E} \left\| \sum _{i=1} ^{N} ϵ_i A_i \right\| &\leq \left( \mathbb{E} \left\| \sum _{i=1} ^{N} ϵ_i A_i \right\|^2 \right) ^{\frac{1}{2}} &\text{Jensen's Inequality} \\ &\approx σ \sqrt{2 \log (n)} \\ &\leq C σ \sqrt{ 1 + \log \left( n \right) } \\ &= C \sqrt{ 1 + \log \left( n \right) } \left\| \sum _{i=1} ^{N} A_i^2 \right\| ^{\frac{1}{2}} \end{align*}3.2. B
We know that for \(X_1, \dots , X_n \) sequence of subgaussian random variables with parameter \(σ\).
\begin{align*} \mathbb{P} \left\{ X \geq a \right\} &= \mathbb{P} \left\{ \exp \left\{ tX \right\} \geq \exp \left\{ t a \right\} \right\} \\ &\leq \frac{\mathbb{E} \left[ \exp \left\{ tX \right\} \right]}{\exp \left\{ ta \right\} } & \text{Markov's Inequality} \\ &\leq \exp \left\{ \frac{σ^2 t^2}{2} - t a \right\} & \text{SubGaussian Definition} \\ \text{Differentiating } t &\Longrightarrow t^* = \frac{a}{σ^2} \\ \mathbb{P} \left( X \geq a \right) &\leq \exp \left\{ -\frac{a^2 }{2 σ^2 } \right\} & \text{Chernoff Inequality} \\ \mathbb{E} \left| X \right| ^{p} &= \int _{0} ^{∞} \mathbb{P} \left( \left| X \right|^p \geq t \right) dt \\ &= \int _{0} ^{∞} \mathbb{P} \left( \left| X \right| \geq t ^{\frac{1}{p}} \right) dt \\ &\leq 2 \int _{0} ^{∞} \exp \left\{ -\frac{ t ^{\frac{2}{p}}}{2 σ^2 } \right\} dt \\ &\leq C σ ^{p} p ^{\frac{p}{2}} \\ \left( \mathbb{E} \left| X \right| ^{p} \right) ^{\frac{1}{p}} &\leq C σ \sqrt{p} \\ \end{align*}Therefore, using similar argument as part (a), we have
\begin{align*} \mathbb{E} \left\| \sum _{i=1} ^{N} ϵ_i A_i \right\| &\leq \left( \mathbb{E} \left\| \sum _{i=1} ^{N} ϵ_i A_i \right\| ^{p} \right) ^{\frac{1}{p}} & \text{Jensen's Inequality} \\ &\approx C σ \sqrt{p} \\ &\leq C σ \sqrt{p + \log \left( n \right)} \\ &= C \sqrt{p + \log \left( n \right)} \left\| \sum _{i=1} ^{N} A_i^2 \right\| ^{\frac{1}{2}} \end{align*}4. 5.4.15
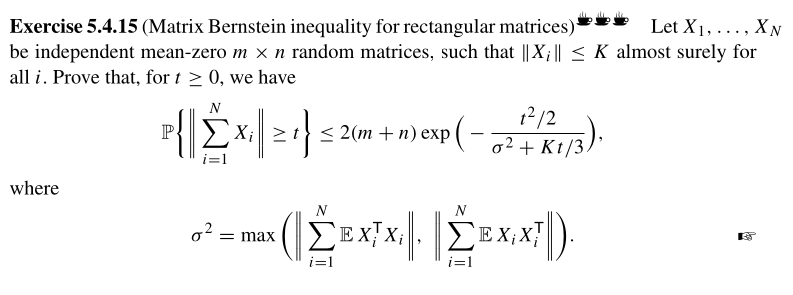

Let
\begin{align*} Z_i = \begin{bmatrix} 0 _{n \times n} & \left( X _{i} ^{T} \right) _{n \times m} \\ \left(X_i \right)_{ m \times n} & 0 _{m \times m} \end{bmatrix} \in \mathbb{S} ^{m + n} \end{align*}
Since the block matrix is symmetric we can apply matrix Bernstein's inequality and \(\left\| Z_i \right\|\leq K\),
For \( Z_1 , \dots , Z_N \in \mathbb{S} ^{m + n}\)
\begin{align*} \mathbb{P} \left\{ \left\| \sum _{i=1} ^{N} Z_i \right\| \geq t \right\} &\leq 2 \left( m + n \right) \exp \left\{ \frac{-t^2/2}{σ^2 + K \left( \frac{t}{3} \right)} \right\} \\ &= 2 \left( m + n \right) \exp \left\{ -c \left( \frac{t^2}{σ^2} \wedge \frac{t}{K} \right) \right\} \end{align*}The non-zero eigenvalues of \(Z_i\) are the same as the singular values of \(X_i\) due to the block matrix structure of \(Z_i\),
\begin{align*} \left\| \sum _ {i=1} ^{N} Z_i \right\| &= \left\| \begin{bmatrix} 0 _{n \times n} & \left( \sum _{i = 1} ^{N} X _{i} ^{T} \right) _{n \times m} \\ \left( \sum _{i=1} ^{N} X_i \right)_{ m \times n} & 0 _{m \times m} \end{bmatrix} \right\| \\ &= \left\| \sum _{i=1} ^N X_i \right\| = \left\| \sum _{i = 1} ^N X_i^T \right\| \end{align*}Therefore
\begin{align*} \mathbb{P} \left\{ \left\| \sum _{i=1} ^{N} X_i \right\| \geq t \right\} &\leq 2 \left( m + n \right) \exp \left\{ \frac{-t^2/2}{σ^2 + K \left( \frac{t}{3} \right)} \right\} \end{align*}Where
\begin{align*} Z_i ^2 = Z_i Z_i &= \begin{bmatrix} 0 _{n \times n} & \left( X _{i} ^{T} \right) _{n \times m} \\ \left(X_i \right)_{ m \times n} & 0 _{m \times m} \end{bmatrix} \begin{bmatrix} 0 _{n \times n} & \left(X_i ^T \right)_{ n \times m} \\ \left( X _{i} \right) _{m \times n} & 0 _{m \times m} \end{bmatrix} \\\ &= \begin{bmatrix} \left( X_i X_i ^T \right)_{ n \times n } & 0 _{n \times m} \\ 0 _{m \times n} & \left( X_i ^T X _{i} \right) _{m \times m} \end{bmatrix} \end{align*} \begin{align*} σ^2 &= \left\| \sum _{i=0} ^{N} \mathbb{E} Z_i^2 \right\| \\ &= \left\| \begin{bmatrix} \sum _{i=0} ^{N} \mathbb{E} \left( X_i X_i ^T \right)_{ n \times n } & 0 _{n \times m} \\ 0 _{m \times n} & \sum _{i=0} ^{N} \mathbb{E} \left( X_i ^T X _{i} \right) _{m \times m} \end{bmatrix} \right\| \\ &= \max \left\{ \left\| \sum _{i=0} ^{N} \mathbb{E} \left[ X_i^T X_i \right] \right\| , \left\| \sum _{i=0} ^{N} \mathbb{E} \left[ X_i X_i^T \right] \right\| \right\} & \text{By definition} \end{align*}